This week I spent most of my time implementing Minimax in Clojure. Upon first approaching the problem I thought my implementation would be similar to my first implementation of minimax in Ruby. But to my surprise the Clojure implementation came out quite different.

The goal of minimax is to have the computer never lose in a game of tic tac toe. So given a board find the optimal move. Here’s a bit of pseudocode for the algorithm.

; for each open spot on the board fill that open spot and determine if the game is over
; if the game is over then determine if the computer or the human won or if the game was tied
  ; if the game is won by the computer return +1 as the score,  
  ; if won by the human return -1 for the score, 
  ; and if tied return 0
; if the game is not over continue to keep playing the game
; if it the computer's turn maximize the scores and if it is the human's turn minimize the scores

This algorithm generates a tree structure, so looking at it from a holistic perspective at each level in the tree we are find the optimal move (whether that’s the min or max of the scores).

Looking at it from this perspective I first started with just generating the next level of the tree. So taking any given board and generating a new sequence of boards with each corresponding open space filled in.

Visually given the computer is marker X and the human is marker O and the open spaces are 5 and 8. How can I generate the next level given a board.

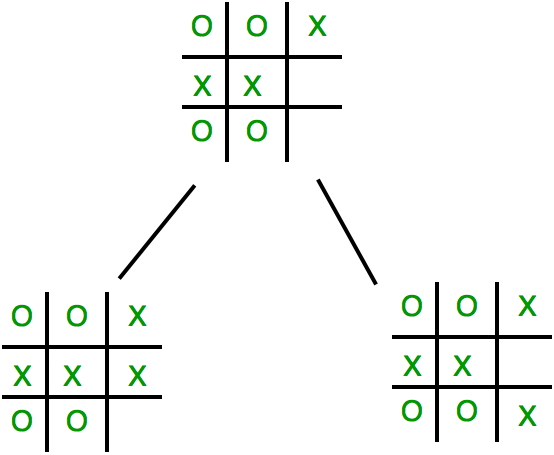
Here’s how I solved this problem

(defn- open-spaces [board]
   (filter number? board))

(defn- generate-boards [current-player-marker board]
  (map #(board/fill-board % board current-player-marker)
       (open-spaces board)))

Given a board I generate a sequences of boards and each value in the sequence is a board with a corresponding open space filled in with the given marker. The next level of the tree in the diagram above is stored in a sequence.

The next step in the algorithm is that for each level in the tree generate the optimal move.

There are two scenarios that could occur in this next step:

1. if the game is over return the score and find the optimal score
2. if the game is not over generate the next level in the tree and find the optimal score

This is essentially the heart of the algorithm. Here’s a diagram of what I’m trying to solve.

Here’s the way I coded in this out in steps

(defn- min-or-max [depth]
  (if (zero? (mod depth 2))
    min
    max))

(defn- optimal-score
  [sequence-boards computer-marker opponent-marker depth]
  (->>
      (map #(retrieve-score % computer-marker opponent-marker depth)
           sequence-boards)
      (apply (min-or-max depth))))

optimal-score takes in a sequence of boards (the next level in the tree) both markers and the depth of the tree (0 if it’s at the top most level, 1 if it’s on the first level, etc.)

The first part of the function with map returns a sequence of scores something like (-1 1 0). It works by calling a function called retrieve-score on each board which will then fetch the score for that specific board. So now that I have a sequence of scores I apply a function called min-or-max which will calculate the minimum of the sequence if the depth is even (the human’s marker) or the maximum if the depth is odd (the computer’s marker).

Ok so how does retreive-score work?

(defn- determine-player-marker [depth computer-marker opponent-marker]
  (if (zero? (mod depth 2))
   computer-marker
   opponent-marker))

(defn- calculate-score [board computer-marker opponent-marker depth]
  (let [winning-marker (game-evaluation/winning-marker board)]
    (if winning-marker
      (if (= winning-marker computer-marker)
        1
        -1)
    0)))

(defn- retrieve-score [board computer-marker opponent-marker depth]
  (if (game-evaluation/game-over? board)
    (calculate-score board computer-marker opponent-marker depth)
    (->
       (determine-player-marker depth computer-marker opponent-marker)
       (generate-boards board)
       (optimal-score computer-marker opponent-marker (inc depth)))))

retrieve-score is just a conditional. It says if the game is over determine the score of that board (1, -1, or 0) if it’s not over figure out which player’s turn it is, generate a new set of boards with each corresponding open space filled in (this is a sequence) and determine the optimal score for that sequence of boards.

Now we have the bulk of the functionality!

The only thing is that ultimately we want a move returned not a score. But based on the functionality defined if we ran our functions we would just receive the best score back, and not the move associated with it.

=> (optimal-score (generate-boards :x [:o :o :x :x :x 5 :o :o 8]) :x :o 1)
; 1

So the next problem is how do I generate the best move. I approached this by thinking that at a depth of 1 that is the only time when we actually care about the move. We don’t necessarily need to know the move on the levels after that.

In a sense we can think of each node of depth 1 generating its own tree and returning a score. In the visual example above the open space of 5 will generate its own tree and return a score and the open space of 8 will generate its own tree and return a score.

So what if I had a map with the keys as the move (on depth 1) and the values as the score of each move on depth 1.

I came up with this function to express this

(defn scores-map [board computer-marker opponent-marker]
 (map #(hash-map %
         (optimal-score
           (lazy-seq (vector (board/fill-board % board computer-marker)))
           computer-marker
           opponent-marker
           1))
         (open-spaces board)))

Given a board and both markers create a hash map with the key as the move and the value as the score of that corresponding subtree. The value is populated by saying for each open space on the board generate a sequence with a new board filled in with the corresponding open space. So in the example above ([:o :o :x :x :x :x :o :o 8]) and ([:o :o :x :x :x 5 :o :o :x]) then on each sequence find the optimal score.

This function returns this

=> (scores-map [:o :o :x :x :x 5 :o :o 8] :x :o)
; ({5 1} {8 0})

So if we go down path 5 we are most likely to win.

This data structure can be manipulated with this function to return to the best move

(defn best-move [move-score-map]
  (->> move-score-map
       (apply merge)
       (apply max-key val)
       (key)))

I can now get the best move for the given board like this

=> (best-move (scores-map [:o :o :x :x :x 5 :o :o 8] :x :o))
; 5

This is just one way to solve the minimax problem. There a numerous ways, but I found this approach the easiest to work with.